boolean algebra

Tweet

Boolean algebra From Wikipedia, the free encyclopedia Jump to: navigation, search For a basic introduction to sets, Boolean operations, Venn diagrams, truth tables, and Boolean applications, see Boolean logic. For an alternative perspective see Boolean algebras canonically defined. In abstract algebra, a Boolean algebra is an algebraic structure (a collection of elements and operations on them obeying defining axioms) that captures essential properties of both set operations and logic operations. Specifically, it deals with the set operations of intersection, union, complement; and the logic operations of AND, OR, NOT. 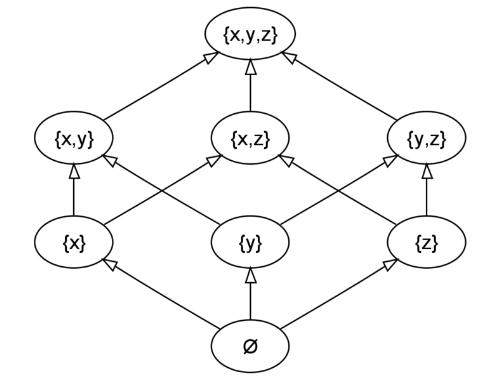For example, the logical assertion that a statement a and its negation ¬a cannot both be true, Boolean lattice of subsets parallels the set-theory assertion that a subset A and its complement AC have empty intersection, Because truth values can be represented as binary numbers or as voltage levels in logic circuits, the parallel extends to these as well. Thus the theory of Boolean algebras has many practical applications in electrical engineering and computer science, as well as in mathematical logic. A Boolean algebra is also called a Boolean lattice. The connection to lattices (special partially ordered sets) is suggested by the parallel between set inclusion, A ? B, and ordering, a = b. Consider the lattice of all subsets of{x,y,z}, ordered by set inclusion. This Boolean lattice is a partially ordered set in which, say,{x} ={x,y}. Any two lattice elements, say p={x,y} and q={y,z}, have a least upper bound, here{x,y,z}, and a greatest lower bound, here{y}. Suggestively, the least upper bound (or join or supremum) is denoted by the same symbol as logical OR, p?q; and the greatest lower bound (or meet or infimum) is denoted by same symbol as logical AND, p?q. The lattice interpretation helps in generalizing to Heyting algebras, which are Boolean algebras freed from the restriction that either a statement or its negation must be true. Heyting algebras correspond to intuitionist (constructivist) logic just as Boolean algebras correspond to classical logic. Contents[hide] 1 Formal definition 2 Examples 3 Order theoretic properties 4 Principle of duality 5 Other notation 6 Homomorphisms and isomorphisms 7 Boolean rings, ideals and filters 8 Representing Boolean algebras 9 Axiomatics for Boolean algebras 10 History 11 See also 12 References 13 External links [edit] Formal definition A Boolean algebra is a set A, supplied with two binary operations (called AND), (called OR), a unary operation (called NOT) and two distinct elements 0 (called zero) and 1 (called one), such that, for all elements a, b and c of set A, the following axioms hold: associativity commutativity absorption distributivity complements The first three pairs of axioms above: associativity, commutativity and absorption, mean that (A,, ) is a lattice. If A is a lattice and one of the above distributivity laws holds, then the second distributivity law can be proven. Thus, a Boolean algebra can also be equivalently defined as a distributive complemented lattice. From these axioms, one can show that the smallest element 0, the largest element 1, and the complement ¬a of any element a are uniquely determined. For all a and b in A, the following identities also follow: idempotence boundedness 0 and 1 are complements De Morgan's laws involution [edit] Examples The simplest Boolean algebra has only two elements, 0 and 1, and is defined by the rules: ? 0 1 0 0 0 1 0 1 ? 0 1 0 0 1 1 1 1 a 0 1 ¬a 1 0 It has applications in logic, interpreting 0 as false, 1 as true, ? as and, ? as or, and ¬ as not. Expressions involving variables and the Boolean operations represent statement forms, and two such expressions can be shown to be equal using the above axioms if and only if the corresponding statement forms are logically equivalent. The two-element Boolean algebra is also used for circuit design in electrical engineering; here 0 and 1 represent the two different states of one bit in a digital circuit, typically high and low voltage. Circuits are described by expressions containing variables, and two such expressions are equal for all values of the variables if and only if the corresponding circuits have the same input-output behavior. Furthermore, every possible input-output behavior can be modeled by a suitable Boolean expression. The two-element Boolean algebra is also important in the general theory of Boolean algebras, because an equation involving several variables is generally true in all Boolean algebras if and only if it is true in the two-element Boolean algebra (which can always be checked by a trivial brute force algorithm). This can for example be used to show that the following laws (Consensus theorems) are generally valid in all Boolean algebras: (a ? b) ? (¬a ? c) ? (b ? c) = (a ? b) ? (¬a ? c) (a ? b) ? (¬a ? c) ? (b ? c) = (a ? b) ? (¬a ? c) Starting with the propositional calculus with ? sentence symbols, form the Lindenbaum algebra (that is, the set of sentences in the propositional calculus modulo tautology). This construction yields a Boolean algebra. It is in fact the free Boolean algebra on ? generators. A truth assignment in propositional calculus is then a Boolean algebra homomorphism from this algebra to{0,1}. The power set (set of all subsets) of any given nonempty set S forms a Boolean algebra with the two operations ?:= ? (union) and ?:= n (intersection). The smallest element 0 is the empty set and the largest element 1 is the set S itself. The set of all subsets of S that are either finite or cofinite is a Boolean algebra. For any natural number n, the set of all positive divisors of n forms a distributive lattice if we write a = b for a| b. This lattice is a Boolean algebra if and only if n is square-free. The smallest element 0 of this Boolean algebra is the natural number 1; the largest element 1 of this Boolean algebra is the natural number n. Other examples of Boolean algebras arise from topological spaces: if X is a topological space, then the collection of all subsets of X which are both open and closed forms a Boolean algebra with the operations ?:= ? (union) and ?:= n (intersection). If R is an arbitrary ring and we define the set of central idempotents by A={ e ? R: e2= e, ex= xe, ?x ? R} then the set A becomes a Boolean algebra with the operations e ? f:= e + f - ef and e ? f:= ef. Certain Lindenbaum–Tarski algebras. [edit] Order theoretic properties Boolean lattice of subsetsLike any lattice, a Boolean algebra (A,, ) gives rise to a partially ordered set (A, =) by defining a = b precisely when a= a b (which is also equivalent to b= a b). In fact one can also define a Boolean algebra to be a distributive lattice (A, =) (considered as a partially ordered set) with least element 0 and greatest element 1, within which every element x has a complement ¬x such that x ¬x= 0 and x ¬x= 1 Here and are used to denote the infimum (meet) and supremum (join) of two elements. Again, if complements in the above sense exist, then they are uniquely determined. The algebraic and the order theoretic perspective can usually be used interchangeably and both are of great use to import results and concepts from both universal algebra and order theory. In many practical examples an ordering relation, conjunction, disjunction, and negation are all naturally available, so that it is straightforward to exploit this relationship. [edit] Principle of duality One can also apply general insights from duality in order theory to Boolean algebras. Especially, the order dual of every Boolean algebra, or, equivalently, the algebra obtained by exchanging and, is also a Boolean algebra. In general, any law valid for Boolean algebras can be transformed into another valid, dual law by exchanging 0 with 1, with, and = with =. [edit] Other notation The operators of Boolean algebra may be represented in various ways. Often they are simply written as AND, OR and NOT. In describing circuits, NAND (NOT AND), NOR (NOT OR) and XOR (eXclusive OR) may also be used. Mathematicians, engineers, and programmers often use + for OR and · for AND (since in some ways those operations are analogous to addition and multiplication in other algebraic structures and this notation makes it very easy to get sum of products form for people who are familiar with normal algebra) and represent NOT by a line drawn above the expression being negated. Sometimes, the symbol~ or! is used for NOT. Here we use another common notation with "meet" for AND, "join" for OR, and ¬ for NOT. [edit] Homomorphisms and isomorphisms A homomorphism between the Boolean algebras A and B is a function f: A ? B such that for all a, b in A:f(a b)= f(a) f(b) f(a b)= f(a) f(b) f(0)= 0 f(1)= 1 It then follows that f(¬a)= ¬f(a) for all a in A as well. The class of all Boolean algebras, together with this notion of morphism, forms a category. An isomorphism from A to B is a homomorphism from A to B which is bijective. The inverse of an isomorphism is also an isomorphism, and we call the two Boolean algebras A and B isomorphic. From the standpoint of Boolean algebra theory, they cannot be distinguished; they differ only in the notation of their elements. [edit] Boolean rings, ideals and filters Every Boolean algebra (A,, ) gives rise to a ring (A, +,*) by defining a + b= (a ¬b) (b ¬a) (this operation is called "symmetric difference" in the case of sets and XOR in the case of logic) and a* b= a b. The zero element of this ring coincides with the 0 of the Boolean algebra; the multiplicative identity element of the ring is the 1 of the Boolean algebra. This ring has the property that a* a= a for all a in A; rings with this property are called Boolean rings. Conversely, if a Boolean ring A is given, we can turn it into a Boolean algebra by defining x y=