Infinitesimal calculus, where it all begins ?
By mor
@stringer321 (5682)
Kiryat Ata, Israel
January 3, 2013 2:09pm CST
Well , that subject is hard and one has to remember every definition and question before making a progress.
Infinitesimal calculus deals with functions, limits, integrals and derivatives.
It has many uses for calculating surface, volume , length of a graph and many other uses.
It all starts with the basic definition of a Set. Do you remember what does it mean B={5,88,44,24,25} ? It means that B is a set and its members are 5,88,44,24,25 (they are taken here from the set of natural numbers).
We can say that 5 belongs to B , and so do 88,44,24 and 25.
So, there are some sets in math that include all the Real numbers and those are all the negative numbers, 0 and all the positive numbers. including the rational and the irrational numbers.
Do you like this subject ? Who could have guess where we can go from those simple definitions and what hard things we will have to learn from there...
2 responses
@StLouisMetroTutoring (678)
• St. Peters, Missouri
4 Jan 13
I made it through calculus. But not easily. With most of the earlier types of math, I fully understood what I was actually doing and I was good at it and enjoyed it. Once I understood it, I learned the process as a means of getting it. Most people understand that multiplication is actually repeated addition. I can understand that 3 X 4 really means that I have 3 groups of 4 objects (or vice versa). I can understand algebra. I understand what we're trying to do. But once I hit trigonometry, no one, including the teachers, could ever explain what we were really doing. When we find the sin of something, what is it that we're finding? Is there a relationship of some type between the number and the answer? The only relationship I know is the sin is what you get when you do these particular steps. All it ever meant to me was following specific procedures to determine something. Nothing but a list of steps. I hated trig and calc for this very reason.
1 person likes this
@stringer321 (5682)
• Kiryat Ata, Israel
4 Jan 13
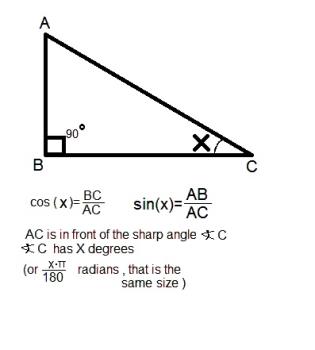
The trigonometry deals with proportions between sections in a triangle (a triangle with a 90 degrees angle). If you have a triangle with a 90 degrees angle, that angle is made of two sections that meet at the same point. Look at the picture.
Trigonometry is only a small part of infinitesimal calculus.
Sin and Cos and Tan are all functions that can be defined on every real number.
You need the trigonometric circle to illustrate the meaning of sin,cos, tan if x is not between 0 and 90 degrees.
@StLouisMetroTutoring (678)
• St. Peters, Missouri
4 Jan 13
Seriously? What is so incredibly difficult about that? Why couldn't any teacher ever explain it all had to do with triangle proportions? Spent a year struggling through trig without ever having this idea and a year in calc without having any idea it had to do with set theory. Would that mean trig is related to geometry? I by no means can all of a sudden do it, but geez, that's all it would have taken. Knowing this, I'm now interested in learning it again.
What are you really doing when you find derivatives and functions and all that? Same thing for me. Just a bunch of steps.
1 person likes this
@stringer321 (5682)
• Kiryat Ata, Israel
6 Jan 13
This is only the basic. What about defining a function, limit of a function where X strives to a certain value...?
The definitions must be well defined and many examples must be learned.
Then, many proves are to be learned and proves are not short. Some creativity is needed there.
Let's see an example I made. I tried to make the example very accurate with a scale of 0.25 on the axis. F(x)=x^2 is the function I draw in the picture. I tried to make the curve as accurate as possible but, it can never be accurate. I made it with a scale of 1/16 on the axis. Now, when we have the curve , we can start to calculate some nice and interesting things like the incline of the curve at a certain point, the area that is under that curve and above the x axis.
I gave some intuitive explanation about how to calculate the area.
To calculate the incline of the graph at a certain point on it, if you don't have a derivative function, you need to calculate the limit with making simple straight lines from one point to the left and one point to the right and make them closer and closer to the point. Also illustrated at the picture. The gray line has it's dy and dx the it's incline is dy/dx. I show dy and dx at the picture.
I really recommend to learn infinitesimal calculus high level. It will help you think logically and you will be able to understand things from the basics.
@JenInTN (27514)
• United States
5 Jan 13
I have a pretty basic understanding but it is not something that comes easy. It is one of the only subjects that I have had to truly study..lol. I spent hours upon hours...well..you get the picture. I can pass it but not with a bright and shiny smile.

1 person likes this
@stringer321 (5682)
• Kiryat Ata, Israel
5 Jan 13
I also didn't pass that subject with a great grade. Only 62/100 , but, it doesn't mean that I didn't understand the material.
They just took the material, and made difficult questions that one needs a lot of research to do before getting the answer.
When I say research I mean like, doing a lot of conclusions from many facts and definitions. Well, that is really a challenge.